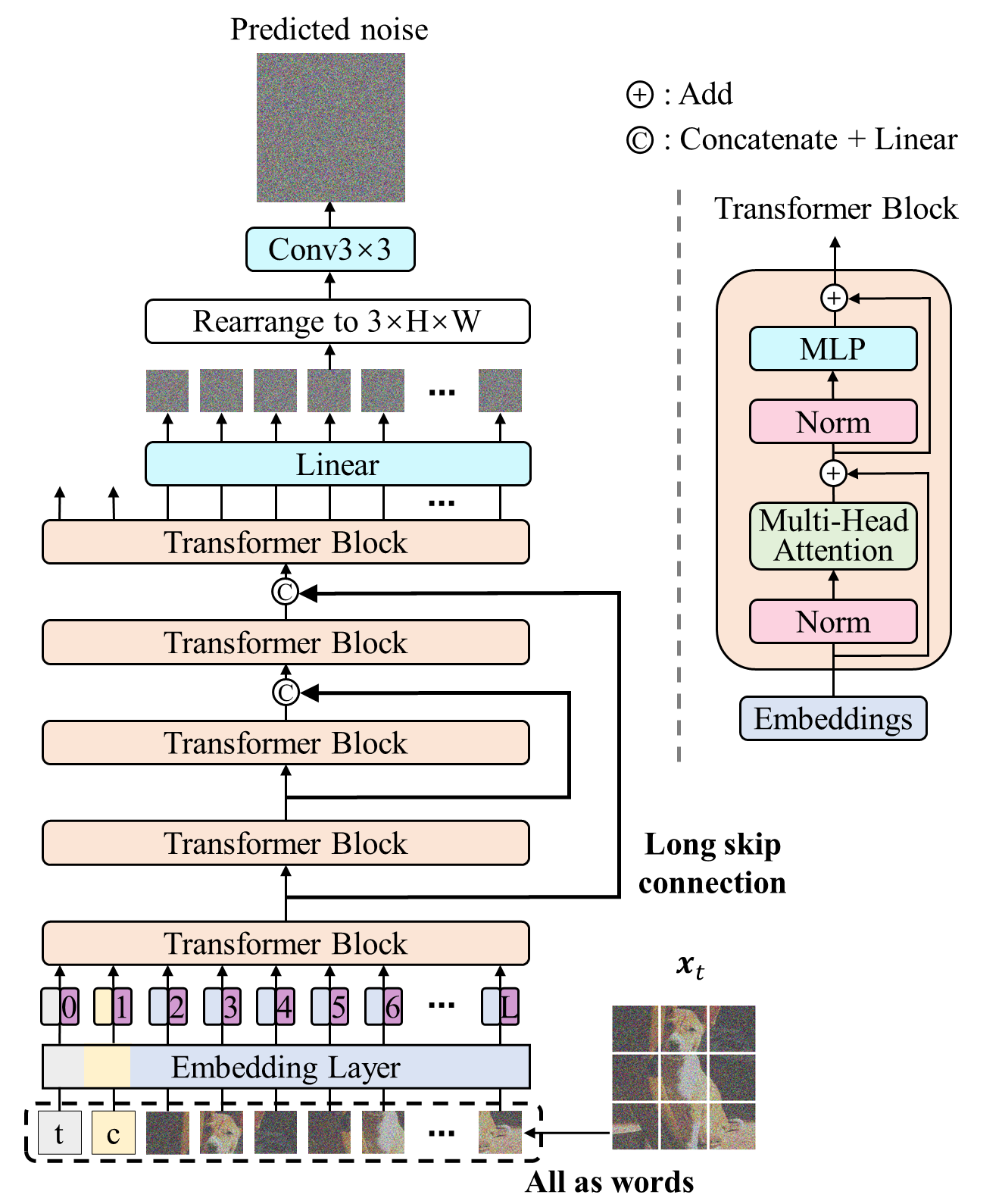
Image 1: The U-ViT architecture from the original paper.
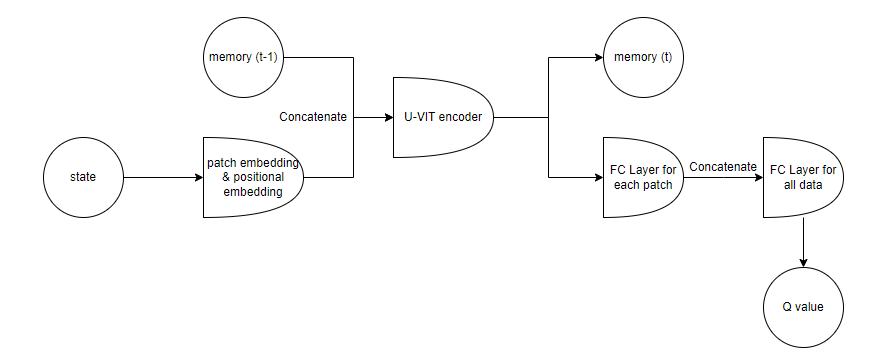
Image 2: The architecture used in the project
DQN is the model that utilizes deep learning architecture to predict the Q value for every action taken by the agent. The Q-value function in the DQN algorithm can be represented as: \begin{equation*} Q(s_t, a_t) \approx r_{t+1} + \gamma \max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) \end{equation*} One of the main problems of the DQN algorithm is that it is hard to converge, and one main reason is that in the DQN loss function, both target Q-values and predicted Q-values contain Q function. In deep learning, the training process can be unstable when the target value is also a function. The target and predicted Q-values are correlated, making it hard for the network to converge. One method to solve the problem is using a separate target network with some delay. Slowing down one network can improve the stability of the whole training process. [1] In some simpler versions, people update the target network every N step, which can also help slow down the target network and support convergence.
In this project, I try to train a relatively complicated deep learning based on the U-ViT model.[2] In the Joint-Embedding Predictive Architecture (JEPA) model, the same problem exists: predicted and target values are from the model as a function. [3] I try to deploy the hypermeters from the training process in the JEPA model to help the DQN training process converge. On the other hand, I add memory as another input to the model to solve the problem of the input state's lack of information.

Image 1: The U-ViT architecture from the original paper.

Image 2: The architecture used in the project
In this project, I added a memory parameter to the model that works similarly to the memory in the GRU model. The memory is a vector with the same length as the width of each patch. The memory is reset to all zero values when resetting the environment. After patch embedding and before transformer blocks, the memory is concatenated to the features and goes through transformer blocks with other features. After the transformer blocks and before the fc layers, the memory is separated from the model and outputted directly. At the same time, the reset features go through the FC layers and generate Q values. The primary goal of using memory is to solve the problem of the learning process being stuck in the first corner of the car racing environment, and the car continuing to spin during the training process. The spinning can also happen in other corners because the state does not provide the correct direction of the route. The problem can be that the input is only the image and lacks more information, like the car's speed and whether the learning process is stuck. When the vehicle is off the track or even the direction is not perfectly following the track, like the situation in which the car is perpendicular to the track, the memory can help the model understand the correct direction and other information that is not provided in the state parameter. This can help the model mainly in training to avoid getting stuck.
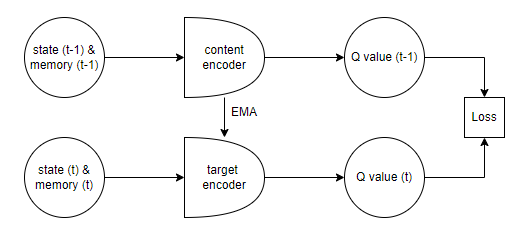
Image 3: The architecture of the training process.
Using a moving average to update the target network started from the teacher-student self-supervised model. Using the moving average can be smoother than updating the target network every N step, and convergence speed can be faster. The target network is used for stable target values during training, preventing the moving target problem where the network changes too quickly during optimization.
The model uses the hyperparameters from the JEPA model. The batch size is 2048, and the optimizer is AdamW. The learning rate is 10^-4, and the weight decay is 0.04. The target network is updated using EMA with a momentum of 0.996. All these parameters are from the JEPA model. The idea is that to stabilize the learning process, the model needs a large batch size and weight decay. These hyperparameters can help to stablize the training process of the network. In comparison, the network is not learnable when using common hypermeters like batch size 32, learning rate 10^-5, and updating the target network every 10 training steps.
I trained the model on the CarRacing-V2 environment from OpenAI Gym in the experiment. The model is in discrete mode, and the action space size is 5. The input state is a 96*96 image with 3 channels. The U-Vit model has 5 layers, as shown in the image, the patch size is 8*8, and the width is 64. The buffer size is 10240, and the model is trained every 1024 steps. The epsilon parameter for the randomness linearly decreases from 1 to 0.1 in the first 2000 training steps and linearly decreases from 0.1 to 0.01 in the next 2000 training steps. One training step means 1024 steps, and the model is trained once. In each training step, the model is trained in 3 epochs, and the gamma in DQN loss is 0.99.
Here is a video showing the result:
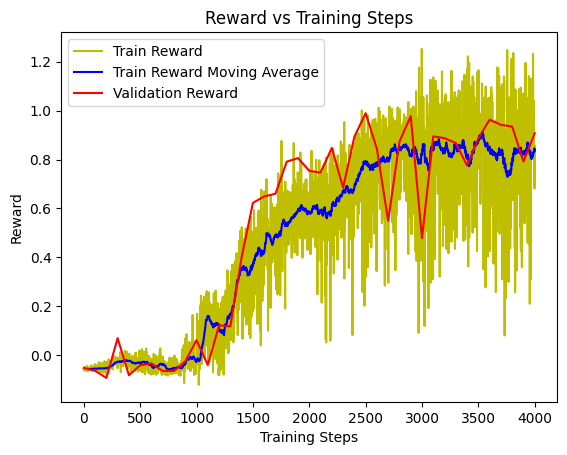
Image 4: The reward curve of the whole training process.
The video shows the result of the training, which showed that the car could successfully follow the track at a relatively high speed. The image shows the average reward per step during the training process. The y-axis is the average reward per environment step, while the reward is from the OpenAI Gym environment. The x-axis is the number of training steps, which means 1024 steps in the environment, and the network is trained in 3 epochs.
In the experiment, the model successfully learned the game rule and followed the track in validation. In my test, the convergence is hard without using the hyperparameters mentioned in the paper. Using batch sizes like 32, the model may be unable to learn the environment. The memory parameter also helps the model avoid sticking in the spinning. With memory, the model can avoid being stuck in the spinning, and the learning curve is smoother and more stable. In my testing, when using other hyperparameters, it is hard to observe continuous loss decrease during 3 epochs of each training step. The research on the JEPA model provides a simple way to set the hyperparameters in DQN.
This project successfully trained a complicated deep reinforcement learning model based on the U-ViT architecture to play the CarRacing-V2 environment in OpenAI Gym. The key aspects that enabled stable training were using a separate target network with exponential moving average updates, incorporating a memory component, and adopting hyperparameters from the JEPA model. Overall, using techniques from self-supervised learning can help train the DQN network.
This research tests the training method on a relatively complicated deep learning network, and the effectiveness on larger models like ViT-Base needs further research. This project introduces one method to record and pass memory between each step, and some more complicated memory architectures, like those applied in LSTM, can be tested in the future. Researches on self-supervised learning provide some useful methods for training a model that can also be used on other supervised model.